问题
解答题
某工厂有214名工人，现要生产1500件产品，每件产品由3个A型零件与1个B型零件配套组成，每个工人加工5个A型零件与3个B型零件所需时间相同．现将全部工人分为两组，分别加工一种零件，同时开始加工．设加工A型零件的工人有x人，在单位时间内每人加工A型零件5k个 （k∈N*），加工完A型零件所需时间为g（x），加工完B型零件所需时间为
h （x）．
（Ⅰ）试比较g（x）与h（x）大小，并写出完成总任务的时间f（x）的表达式；
（Ⅱ）怎样分组才能使完成任务所需时间最少？
答案
解：（Ⅰ）由题意，A型零件共需要4500个，B型零件共需要1500个，
加工B型零件的工人有214﹣x人，单位时间内每人加工B型零件3k个，
所以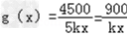 
，
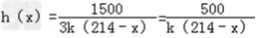∴g（x）﹣h（x）=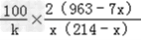 
∵0＜x＜214，且x∈N*，
∴当1≤x≤137（x∈N*）时，g（x）＞h（x）；
当137≤x≤213（x∈N*）时，g（x）＜h（x）；
∴f（x）=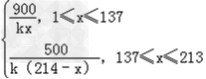
（其中x∈N*）
（Ⅱ）分组才能使完成任务所需时间最少，即求当x为何值时，f（x）最小
∵当1≤x≤137（x∈N*）时，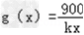
为减函数；
当137≤x≤213（x∈N*）时，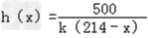 
为增函数
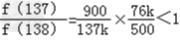
∴x=137时，f（x）最小
即加工A型零件137人，加工B型零77人，完成任务所需时间最少