问题
解答题
下表给出了代数式x2+bx+c与x的一些对应值:
(2)代数式x2+bx+c是否有最小值?如果有,求出最小值;如果没有,请说明理由; (3)设y=x2+bx+c的图象与x轴的交点为A、B两点(A点在B点左侧),与y轴交于点C,P点为线段AB上一动点,过P点作PE∥AC交BC于E,连接PC,当△PEC的面积最大时,求P点的坐标. |
答案
(1)由题意知:
解得b=-4(1分)c=3 4+2b+c=-1
| x | … | -1 | 0 | 1 | 2 | 3 | 4 | … |
| X2+bx+c | … | 8 | 3 | 0 | -1 | 0 | 3 | … |
∴x2-4x+3有最小值,最小值为-1;(3分)
(3)由(1)可知,点A、B的坐标分别为(1,0),(3,0)、设点P的坐标为(x,0),过点E作EM⊥x轴于点M,
∵PE∥AC,∴△EPB∽△CAB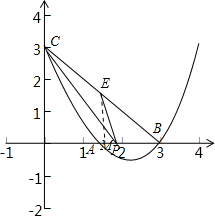
∵EM、CO分别为△EPB与△CAB边上的高,
∴
=EM CO
(4分)PB AB
∵CO=3,AB=2,PB=3-x,∴EM=
(3-x)(5分)3 2
∴S△PEC=S△PBC-S△PBE=
PB•CO-1 2
PB•EM(6分)1 2
=
(3-x)[3-1 2
]=-3(3-x) 2
(x-2)2+3 4
(7分)3 4
∴当x=2时,S有最大值
;3 4
∴当点P的坐标为(2,0)时,△PEC的面积最大.(8分)