问题
解答题
已知点P,Q,R分别在△ABC的边AB,BC,CA上,且BP=PQ=QR=RC=1,求△ABC的面积的最大值.
答案
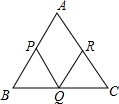
由正弦定理得:BQ=2cosB,CQ=2cosC,
由上可推出BC=2(cosB+cosC),
AB=BC
,AC=BCsinC sinA
,sinB sinA
∴S△ABC=
×AB×AC×sinA,1 2
∵三边固定,当面积最大时,sinA=1,∠A=90°,
又∠APR=∠ARP=∠QPR=∠QRP
所以△APR相似于△QPR
因为PR边公用,所以AP=AR=QP=QR=1
AB=AC=2,
∴S△ABC=
×AB×AC×sinA=2.1 2
