问题
解答题
我们知道任何实数的平方一定是一个非负数,即:
(a+b)2≥0,且-(a+b)2≤0。据此,我们可以得到下面的推理:
∵x2+2x+3=(x2+2x+1)+2=(x+1)2+2,而(x+1)2≥0
∴(x+1)2+2≥2,故x2+2x+3的最小值是2。
试根据以上方法判断代数式3y2-6y+11是否存在最大值或最小值?若有,请求出它的最大值或最小值。
答案
解:原式=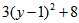
∵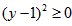 ,∴
,∴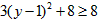 ,
,
所以有最大值,最大值为8。
