问题
解答题
已知函数f(x)=x3-x，
（1）设M(λ0，f(λ0))是函数图象上的一点，求点M处的切线方程；
（2）证明过点N（2，1）可以作曲线f(x)=x3-x的三条切线。
答案
（1）解：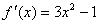
，
过点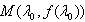
的切线斜率为
，
切线方程为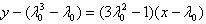
，
即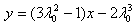
；
（2）证明：由（1）知曲线上点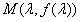
处的切线为
，
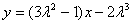若切线过点N（2，1），则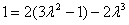
，即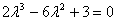
，
若过N有三条切线等价于方程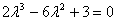
有三个不同的解，
设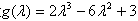
，
，
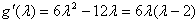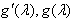随λ变化如下表：
g（λ）在R上只有一个极大值和一个极小值，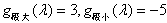
，
∴g（λ）=0有3个不同解，即方程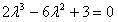
有3个不同解，
即过点N可以作曲线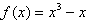
的三条切线。