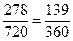问题
解答题
从分别写有0，1，2，3，4，5，6的七张卡片中，任取4张，组成没有重复数字的四位数，计算：
(1)这个四位数是偶数的概率；
(2)这个四位数能被9整除的概率；
(3)这个四位数比4510大的概率。
答案
（1）组成的四位数为偶数的概率为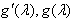
，（2）能被9整除的四位数的概率为
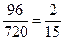，（3）四位数且比4510大的概率为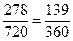
（1）组成的所有四位数共有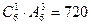
个。四位偶数有：个位是0时有
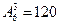,个位不是0时有
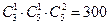,共有120+300=420个.
组成的四位数为偶数的概率为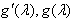
(2)能被9整除的数，应该各位上的数字和能被9整除.数字组合为：1，2，6，0 1，3，5，0 2，4，5，0 3，4，5，6 2，3，4，0 此时共有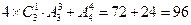
.
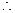能被9整除的四位数的概率为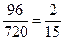
(3)比4510大的数分别有：千位是4，百位是5时，有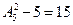
;千位是4，百位是6时，有
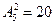;千位大于4时，有
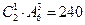;故共有240+20+18=278.
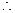四位数且比4510大的概率为