问题
解答题
设函数f(x)=xekx(k≠0)，
(Ⅰ)求曲线y=f(x)在点(0，f(0))处的切线方程；
(Ⅱ)求函数f(x)的单调区间；
(Ⅲ)若函数f(x)在区间(-1，1)内单调递增，求k的取值范围．
答案
解：(Ⅰ)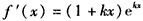
，f′(0)=1，f(0)=0，
曲线y=f(x)在点(0，f(0))处的切线方程为y=x。
(Ⅱ)由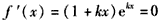
，得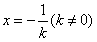
，
若k＞0，则当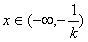
时，f′(x)＜0，函数f(x)单调递减；
当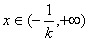
时，f′(x)＞0，函数f(x)单调递增；
若k＜0，则当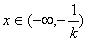
时，f′(x)＞0，函数f(x)单调递增；
当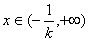
时，f′(x)＜0，函数f(x)单调递减；
(Ⅲ)由(Ⅱ)知，若k＞0，则当且仅当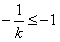
，即k≤1时，函数f(x)在(-1，1)内单调递增；
若k＜0，则当且仅当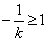
，即k≥-1时，函数f(x)在(-1，1)内单调递增；
综上可知，函数f(x)在区间(-1，1)内单调递增时，k的取值范围是[-1，0)∪(0，1]。