问题
解答题
已知f(x)=ln(x+2)-x2+bx+c，
(1)若函数f(x)在x=1处的切线与直线3x+7y+2=0垂直，且f(-1)=0，求函数f(x)的解析式；
(2)若f(x)在区间[0，2]上单调递减，求b的取值范围．
答案
解：(1)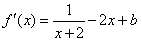
，
由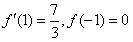
得b=4，c=5，
所以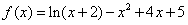
。
(2)
，
设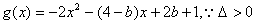
恒成立，
∴g(x)=0必有两根，
∵f(x)在区间[0，2]上单调递减，
∴g(x)在[0，2]上值恒非正，
∴
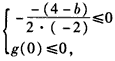或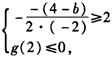
，
解得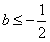
，
故当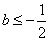
时，f(x)在[0，2]上单调递减．