解：（1）f'（x）=3x²+4ax+b，g'（x）=2x-3

由于曲线y=f（x）与y=g（x）在点（2，0）处有相同的切线，

故有f（2）=g（2）=0，f（2）=g'（2）=1

由此得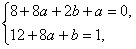

解得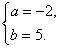

所以a=-2，b=5，

切线l的方程为x-y-2=0。

（2）由（1）得f（x）=x³-4x²+5x-2，

所以f（x）+g（x）=x³-3x²+2x

依题意，方程x（x²-3x+2-m）=0有三个互不相同的实根0、x₁、x₂，

故x₁、x₂是方程x²-3x+2-m=0的两相异的实根，

所以△=9-4（2-m）>0，即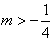

又对任意的x∈[x₁，x₂]，f（x）+g（x）＜m（x-1）成立，

特别地，取x=x₁时，f（x₁）+g（x₁）-mx₁＜-m成立，得m＜0

由韦达定理，可得x₁+x₂=3>0，x₁x₂=2-m>0，

故0＜x₁＜x₂

对任意的x∈[x₁，x₂]，有x-x₂≤0，x-x₁≥0，x>0，

则f（x）+g（x）-mx=x（x-x₁）（x-x₂）≤0

又f（x₁）+g（x₁）-mx₁=0，

所以函数f（x）+g（x）-mx在x∈[x₁，x₂]的最大值为0

于是当m＜0时，对任意的x∈[x₁，x₂]，f（x）+g（x）＜m（x-1）恒成立，

综上，m的取值范围是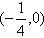。