解：（1）因 f（x）=x³+ax²+bx+1，故f'（x）=3x²+2ax+b

令x=1，得f'（1）=3+2a+b，由已知f'（1） =2a，

因此3+2a+b =2a，解得b=-3

又令x=2，得f'（2）=12+4a+b，由已知f'（2）=-b，

因此12+ 4a+b=-b，解得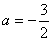

因此，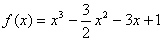

从而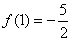

又因为，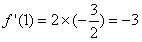

故曲线y=f（x）在点（1，f（1）） 处的切线方程为

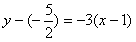，即6x+2y-1=0。

（2）由（1）知g（x）=（3x²-3x-3）e^-x，

从而有g'（x）=（-3x²+9x）e^-x，

令g'（x）=0，得-3x²+9x=0，解得x₁=0，x₂=3

当x∈（-∞，0）时，g'（x）＜0，故g（x）在（-∞，0）上为减函数；

当x∈（0，3）时，g'（x）>0，故g（x）在（0，3）上为增函数；

当x∈（3，+∞）时，g'（x）＜0，故g（x）在（3，+∞）上为减函数；

从而函数g（x）在x₁=0处取得极小值g（0）=-3，

在x₂=3处取得极大值g（3）=15e^-3。