A、B两列火车,在同一轨道上同向行驶,A车在前,其速度vA="10" m/s,B

问题计算题

A、B两列火车,在同一轨道上同向行驶,A车在前,其速度v_A="10" m/s,B车速度v_B="30" m/s.因大雾能见度很低,B车在距A车600 m时才发现前方有A车,这时B车立即刹车,但B车要经过1800 m才能够停止.问：

(1) A车若按原速前进,两车是否会相撞？若会相撞,将在何时何地？

(2) 若B车司机在刹车后发出信号，A车司机接收到信号后以加速度a₁=0.25m/s²加速前进，已经比B车刹车时刻晚了Δt="8" s, 问是否能避免事故？若能够避免，求两车的最小距离。

答案

解：(1)为了求解简便,我们先以A车为参考系,设在B车恰能追上A车的情况下,A、B两车之间的初始间距为s₀,则

(v_B－v_A)²=2as₀ ①

再以地面为参考系,设B车的最大滑行距离为s₁,则

v_B²=2as₁ ②

解①②两式可得s₀="800" m

因为s₀＞600 m,所以两车一定相撞.设两车经时间t相撞,则有：

vt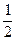－at²=v_At+s ③

由②式得：a="0.25" m/s²,代入③式得t="40" s.（t=120s舍去）

设相撞地点距B车刹车地点s_B,则有s_B=v_At+s=10×40 m+600 m="1000" m.

(2)设B车减速t₁秒时两车的速度相同：

v_B -at₁= v_A +a₁(t₁-Δt)

代入数解得t₁=44s

在此过程中： S_B = v_B t₁-at₁²/2 ="1078" m

S_A= v_A t₁+a₁(t₁-Δt)²/2= 602m

S_A +600＞S_B不会发生撞车事故。

此时ΔS= S_A +600- S_B =124m