（8分）如图所示，光滑水平面上有一块木板，质量M="2.0" kg，长度L=1.0m。在木板的最右端有一个小滑块（可视为质点），质量m="1.0" kg。小滑块与木板之间的动摩擦因数μ=0.2。开始时它们都处于静止状态。某时刻起对小滑块施加一个F="5.0" N水平向左的恒力，此后小滑块将相对木板滑动。取g ="10" m/s2。求：
（1）小滑块从木板右端运动到左端所用的时间t；
（2）小滑块从木板右端运动到左端的过程中，恒力F对小滑块所做的功W；
（3）如果想缩短小滑块从木板右端运动到左端所用的时间t，只改变木板的质量M，请你通过计算，判断木板的质量M应该增大还是减小？
（1）小滑块受到水平向左的恒力F和水平向右的滑动摩擦力作用，向左做匀加速直线运动，所受滑动摩擦力 f =" μmg" = 0.2×1.0×10 =" 2.0" (N)
根据牛顿第二定律，小滑块的加速度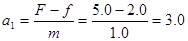 
(m/s2)
木板所受向左的滑动摩擦力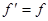 
，向左做匀加速直线运动。根据牛顿第二定律，木板的加速度 
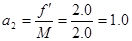(m/s2)
在小滑块从木板右端运动到左端所用的时间为t内，小滑块的位移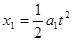 
木板的位移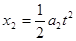 
由几何关系可知L = x1 – x2
解得 t =" 1.0" （s）
(2) 小滑块的位移
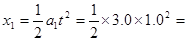1.5 (m)
恒力F对小滑块所做的功
W = Fx1 =" 5.0×1.5" =" 7.5" (J)
(3)由于x1 – x2 = L，
即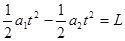
将（1）中各式代入，有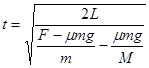
若只改变M，则M增加时，t 减小。
（1）小滑块受到水平向左的恒力F和水平向右的滑动摩擦力作用，向左做匀加速直线运动，求出加速度，木板所受向左的滑动摩擦力向左做匀加速直线运动，求出加速度，根据位移关系即可求出时间；
（2）求出小滑块的位移，根据恒力做功公式即可求解；
（3）根据位移差为L，求出时间t与质量的关系即可求解．