问题
解答题
已知直线l1为曲线y=x2+x-2在点(1,0)处的切线,l2为该曲线的另一条切线,且l1⊥l2,
(Ⅰ)求直线l2的方程;
(Ⅱ)求由直线l1、l2和x轴所围成的三角形的面积。
答案
解:(Ⅰ)y′=2x+1,
直线l1的方程为y=3x-3,
设直线l2过曲线y=x2+x-2上的点B(b,b2+b-2),
则l2的方程为y=(2b+1)x-b2-2,
因为l1⊥l2,则有2b+1=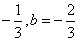 ,
,
所以直线l2的方程为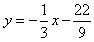 。
。
(Ⅱ)解方程组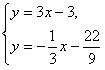 ,得
,得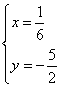 ,
,
所以直线l1和l2的交点的坐标为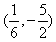 ,
,
l1、l2与x轴交点的坐标分别为(1,0)、 ,
,
所以所求三角形的面积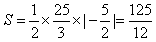 。
。
