问题
解答题
咖啡馆配制两种饮料，甲种饮料用奶粉、咖啡、糖分别为9g、4g、3g，乙种饮料用奶粉、咖啡、糖分别为4g、5g、10g。已知每天使用原料的限额为奶粉3600g、咖啡2000g、糖3000g，如果甲种饮料每杯能获利0.7元，乙种饮料每杯能获利1.2元，每天在原料的使用限额内饮料能全部售出，每天应配制两种饮料各多少杯能获利最大？
答案
解：设每天应配制甲种饮料x杯，乙种饮料y杯，咖啡馆每天获利z元，x、y满足约束条件：
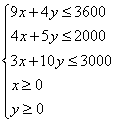
在平面直角坐标系内作出可行域，如下图：
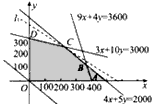
考虑z=0.7x+1.2y，将它变形为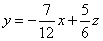
这是斜率为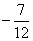
,随z变化的一组平行直线，
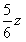是直线在y轴上的截距
当直线截距最大时，z的值最大，即在满足约束条件时目标函数z=0.7x+1.2y取得最大值，由图可见，当直线z=0.7x+1.2y经过可行域上的点C时，截距最大，即z最大
解方程组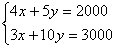
得点C的坐标为（200，240），
所以，每天应配制甲种饮料200杯，乙饮料240杯，能使该咖啡馆获利最大。