问题
解答题
已知函数f(x)=x2-1与函数g(x)=alnx(a≠0)，
(Ⅰ)若f(x)，g(x)的图象在点(1，0)处有公共的切线，求实数a的值；
(Ⅱ)设F(x)=f(x)-2g(x)，求函数F(x)的极值．
答案
解：(Ⅰ)因为f(1)=0，g(1)=0，
所以点(1，0)同时在函数f(x)，g(x)的图象上，
因为f(x)=x2-1，g(x)=alnx，f′(x)=2x，g′(x)=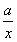
，
由已知，得f′(1)=g′(1)，所以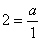
，即a=2．
(Ⅱ)因为F(x)=f(x)-2g(x)=x2-1-2alnx(x＞0)，
所以F′(x)=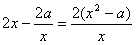
，
当a＜0时，因为x＞0，且x2-a＞0，所以F′(x)＞0对x＞0恒成立，
所以F(x)在(0，+∞)上单调递增，F(x)无极值；
当a＞0时，令F′(x)=0，解得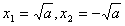
(舍)，
所以当x＞0时，F′(x)，F(x)的变化情况如下表：
所以当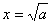
时，F(x)取得极小值，且
；
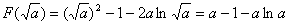综上，当a＜0时，函数F(x)在(0，+∞)上无极值；当a＞0时，函数F(x)在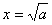
处取得极小值a-1-alna。