问题
解答题
某乡镇为了盘活资本，优化组合，决定引进资本拯救出现严重亏损的企业。长年在外经商的王先生为了回报家乡，决定投资线路板厂和机械加工厂。王先生经过预算，如果引进新技术在优化管理的情况下，线路板厂和机械加工厂可能的最大盈利率分别为95%和80%，可能的最大亏损率分别为30%和10%。由于金融危机的影响，王先生决定最多出资100万元引进新技术，要求确保可能的资金亏损不超过18万元．问王先生对线路板厂和机械加工厂各投资多少万元，才能使可能的盈利最大？
答案
解：设王先生分别用x万元、y万元投资线路板厂和机械加工厂两个项目，盈利为z万元，
由题意知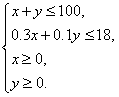
目标函数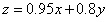
，
上述不等式组表示的平面区域如图所示，阴影部分（含边界）即可行域，
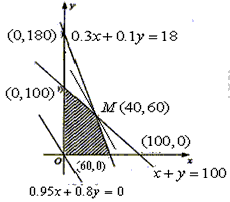
作直线l0：0.95x+0.8y=0，并作平行于直线l0的一组直线
与可行域相交，其中有一条直线经过可行域上的M点，且与直线0.95x+0.8y=0的距离最大，
这里M点是直线x+y=100和0.3x+0.1y=18的交点，
解方程组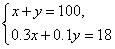
，得x=40，y=60，
此时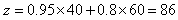
（万元），
所以当x=40，y=60时z取得最大值。
答：王先生用40万元投资线路板厂、60万元机械加工厂，才能在确保亏损不超过18万元的前提下，使可能的盈利最大为86万元。
