解：（Ⅰ）由已知得f′(x)=3x²-2x-1，

又f′(2)=7，

所求切线方程是7x-y-12=0；

（Ⅱ）因为f′(x)=3x²-2x-1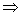f′(x)=0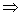x₁=1，x₂=，

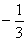又函数f(x)的定义域是所有实数，则x变化时，f′(x)的变化情况如下表：

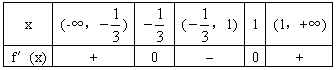
所以当x=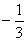时，函数f(x)取得极大值为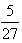；当x=1时，函数f(x)取得极小值为-1。