问题
问答题
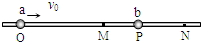
如图所示,光滑绝缘杆上套有两个完全相同、质量都是m的金属小球a、b,a带电量为q(q>0),b不带电.M点是ON的中点,且OM=MN=L,整个装置放在与杆平行的匀强电场中.开始时,b静止在杆上MN之间的某点P处,a从杆上O点以速度v0向右运动,到达M点时速度为3v0/4,再到P点与b球相碰并粘合在一起(碰撞时间极短),运动到N点时速度恰好为零.求:
(1)电场强度E的大小和方向;
(2)a、b两球碰撞中损失的机械能;
(3)a球碰撞b球前的速度v.
答案
(1)a球从O到M,
由动能定理,则有,WOM=-qEL=
m(1 2
v0)2-3 4
m1 2 v 20
解得:E=7m v 20 32qL
方向向左
(2)设碰撞中损失的机械能为△E,对a、b球从O到N的全过程应用能的转化和守恒定律
-qE2L-△E=0-
mv021 2
则碰撞中损失的机械能为△E=
m1 2
-v 20
m7 16
=v 20
m1 16 v 20
(3)设a与b碰撞前后的速度分别为v、v′,
则 动量守恒定律,mv=2mv’
减少的动能△E=
mv2-1 2
2mv′2=1 2
m1 16 v 20
解得:v=
v 01 2
答:(1)电场强度:E=
和方向向左;7m v 20 32qL
(2)a、b两球碰撞中损失的机械能
m1 16
;v 20
(3)a球碰撞b球前的速度
.v0 2
