问题
解答题
已知下 * * 个函数：①y=10；②y=x；③y=2x。
（1）求这三个函数在任一点x=x0处的切线方程；
（2）若这三个函数都是做直线运动的物体的路程y关于时间x的函数，试分别判断该物体的运动状态。
答案
解：分别对三个函数求导数得①y′=10′=0，②y′=x′=1，③y′=（2x）′=2，
（1）①∵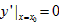
，即点（x0，10）处的切线斜率为0，
∴在点x=x0处切线方程为y-10=0，即y=10，
②∵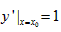
，且x=x0时y=x0，
∴在点x=x0处的切线方程为y-x0=x-x0，即y=x，
③∵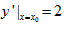
，且x=x0时y=2x0，
∴在x=x0处切线方程为y-2x0=2（x-x0），
即y=2x；
（2）①y′=0，说明物体运动速度为0，因此该物体始终处于静止状态，
②y′=1，说明物体运动速度为1，因此该物体做匀速直线运动，
③y′=2，说明物体运动速度为2，因此该物体做匀速直线运动。