问题
解答题
已知函数f(x)=x4-3x2+6,
(Ⅰ)讨论f(x)的单调性;
(Ⅱ)设点P在曲线y=f(x)上,若该曲线在点P处的切线l通过坐标原点,求l的方程。
答案
解:(Ⅰ)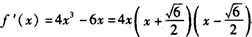 ,
,
当x∈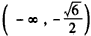 和x∈
和x∈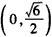 时,f′(x)<0;
时,f′(x)<0;
当x∈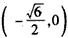 和x∈
和x∈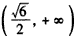 时,f′(x)>0;
时,f′(x)>0;
因此,f(x)在区间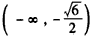 和
和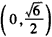 是减函数,
是减函数,
f(x)在区间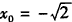 和
和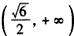 是增函数。
是增函数。
(Ⅱ)设点P的坐标为(x0,f(x0)),
由l过原点知,l的方程为y=f′(x0)x,
因此,f(x0)=x0f′(x0),
即:x04-3x02+6-x0(4x03-6x0)=0,
整理得(x02+1)(x02-2)=0,解得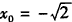 或
或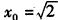 ,
,
因此切线l的方程为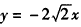 或
或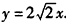 。
。
