解：（1）由题意知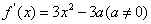

∵曲线y= f（x）在点（2，f（2））处与直线y=8相切

∴

∴

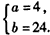
（2）∵，

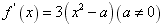∴①当a＜0时，f′（x）>0，函数f（x）在（-∞，+∞）上单调递增，此时函数f（x）没有极值点。

②当a>0时，由f′（x）=0可得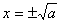

i）当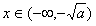时，f′（x）>0，函数f（x）单调递增；

ii）当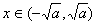时，f′（x）＜0，函数f（x）单调递减；

iii）当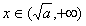时，f′（x）>0，函数f（x）单调递增

综上可知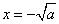，是f（x）的极大值点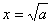，是f（x）的极小值点。