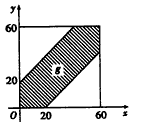
解：在平面上建立如图所示的直角坐标系，

直线x=60，直线y=60，x轴、y轴围成一个正方形区域G，

设甲12时x分到达会面地点，乙12时y分到达会面地点，

这个结果与平面上的点（x，y）对应，

于是试验的所有可能结果就与G中的所有点一一对应，

由题意知，每一个试验结果出现的可能性是相等的，

因此，试验属于几何概型。

当且仅当甲、乙两人到达会面地点的时间差不超过20min 时，

甲、乙两人能会面，即|y-x|≤20，

因此，图中的阴影区域g就表示“甲、乙两人能会面”，

容易求得g的面积为60²-40²=2000，G的面积为3600，

由几何概型的概率计算公式，

“甲、乙两人能会面”的概率P=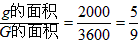。