问题
解答题
（1）已知不同的实数a，b∈{﹣1，1，2}，求直线y=ax+b不经过第四象限的概率；
（2）若a∈[﹣2，2]，b∈[﹣1，1]，求直线ax+by+1=0（a、b不同时为0）与圆x2+y2=1有公共点的概率．
答案
解：（1）由题意知本题是一个古典概型，试验发生包含的事件a，b∈{﹣1，1，2}（a≠b）
得到（a，b）的取值所有可能的结果有：（﹣1，1）；（﹣1，2）；（1，﹣1）；（1，2）；（2，﹣1）；（2，1）共6种结果．
而当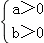
时，直线不经过第四象限，
符合条件的（a，b）有2种结果，
∴直线不过第四象限的概率P=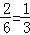
（2）由题意知本题是一个几何概型，∵直线ax+by+1=0与圆x2+y2=1有公共点
∴
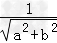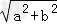≤1
≥1
a2+b2≥1
a∈[﹣2，2]，b∈[﹣1，1]，
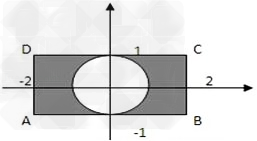
则（a，b）对应的区域为矩形ABCD（如图）
满足条件a2+b2≥1的（a，b）对应的区域为图中阴影部分．
∴直线ax+by+1=0与圆x2+y2=1有公共点的概率
P=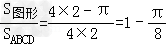
．
