问题
解答题
已知抛物线y=ax2+bx+c过点(1,1),且在点(2,-1)处与直线y=x-3相切,求a、b、c的值。
答案
解:∵y=ax2+bx+c过点(1,1),
∴a+b+c=1,
∵y′=2ax+b,
∴曲线过点P(2,-1)的切线的斜率为4a+b =1,
又曲线过点(2,-1),
∴4a+2b+c=-1,
由 解得
解得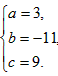
∴a、b、c的值分别为3、-11、9。
已知抛物线y=ax2+bx+c过点(1,1),且在点(2,-1)处与直线y=x-3相切,求a、b、c的值。
解:∵y=ax2+bx+c过点(1,1),
∴a+b+c=1,
∵y′=2ax+b,
∴曲线过点P(2,-1)的切线的斜率为4a+b =1,
又曲线过点(2,-1),
∴4a+2b+c=-1,
由 解得
解得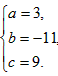
∴a、b、c的值分别为3、-11、9。