问题
解答题
求曲线y=x3在点（3，27）处的切线与两坐标轴所围成的三角形的面积。
答案
解：∵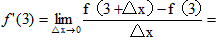
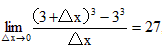
∴曲线在点（3，27）处的切线方程为y-27=27（x-3），即y=27x-54，
此切线与x轴、y轴的交点分别为（2，0）、（0，-54），
∴切线与两坐标轴围成的三角形的面积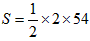
=54。
搜题请搜索小程序“爱下问搜题”
求曲线y=x3在点（3，27）处的切线与两坐标轴所围成的三角形的面积。
解：∵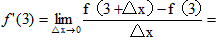
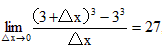
∴曲线在点（3，27）处的切线方程为y-27=27（x-3），即y=27x-54，
此切线与x轴、y轴的交点分别为（2，0）、（0，-54），
∴切线与两坐标轴围成的三角形的面积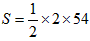=54。