问题
解答题
已知抛物线C1：y=x2+2x和C：y=-x2+a，如果直线l同时是C1和C2的切线，称l是C1和C2的公切线，公切线上两个切点之间的线段，称为公切线段。
（1）a取什么值时，C1和C2有且仅有一条公切线？写出此公切线的方程；
（2）若C1和C2有两条公切线，证明相应的两条公切线段互相平分。
答案
解：（1）函数y=x2+2x的导数y′=2x+2，
曲线C1在点P（x1，x21+2x1）的切线方程是：y-（x12+2x1）=（2x1+2）（x-x1），
即y=（2x1+2）x-x12 ①
函数y=-x2+a的导数y′=-2x，
曲线C2在点Q（x2，-x22+a）的切线方程是y-（-x22+a）=-2x2（x-x2）
即y=-2x2x+x22+a ②
如果直线l是过P和Q的公切线，则①式和②式都是l的方程，
所以x1+1=-x2，-x12=x22+a
消去x2得方程2x12+2x2+1+a=0
若判别式△=4-4×2（1+a）=0时，
即a=-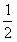
时，解得x1=-
，
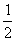此时点P与Q重合，
即当a=-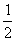时C1和C2有且仅有一条公切线，由①得公切线方程为y=x-
。
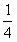（2）由（1）可知，当a＜-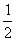
时C1和C2有两条公切线
设一条公切线上切点为：P（x1，y1）， Q（x2 ，y2）
其中P在C1上，Q在C2上，
则有x1+x2=-1，y1+y2=x12+2x1+（-x22+a）=x21+2x1-（x1+1）2+a=-1+a，
线段PQ的中点为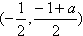
同理，另一条公切线段P′Q′的中点也是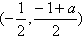
所以公切线段PQ和P′Q′互相平分。