问题
填空题
已知点P在曲线y=
|
答案
根据题意得f′（x）=-
，4ex e2x+2ex+1
∵k=-
≥ -4 ex+
+21 ex
=-1，4 2+2
且k＜0
则曲线y=f（x）上切点处的切线的斜率k≥-1，
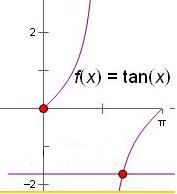
又∵k=tanα，结合正切函数的图象
由图可得α∈[
，π)，3π 4
故答案为：[
，π)．3π 4
搜题请搜索小程序“爱下问搜题”
已知点P在曲线y=
|
根据题意得f′（x）=-
，4ex e2x+2ex+1
∵k=-
≥ -4 ex+
+21 ex
=-1，4 2+2
且k＜0
则曲线y=f（x）上切点处的切线的斜率k≥-1，
又∵k=tanα，结合正切函数的图象
由图可得α∈[
，π)，3π 4
故答案为：[
，π)．3π 4