搜题请搜索小程序“爱下问搜题”
问题 填空题
在面积为1的正方形ABCD内部随机取一点P，则△PAB的面积大于等于
1
4
的概率是______．
答案

设正方形ABCD中，E、F分别为AD、BC的中点

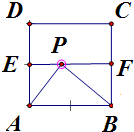
∵四边形ABCD是正方形，E、F分别为AD、BC的中点

∴EF∥AB且EF=AB，可得四边形ABFE是矩形

∵正方形ABCD面积为1，∴AB=1且AE=

1
2
AD=
1
2

当点P落在线段EF上时，△PAB的面积等于矩形ABFE面积的一半，

此时S△ABP=

1
2
S矩形ABFE=
1
4

因此，当点P落在正方形ABCD内部，且在线段EF上或EF的上方时，

可使△PAB的面积大于等于

1
4

∴△PAB的面积大于等于

1
4
的概率为P=
SCDEF
SABCD
=
1
2

故答案为：

1
2

判断题

非宗教团体、非宗教活动场所不得组织、举行宗教活动，但可以接受宗教性的捐献。（）
查看答案
单项选择题

一般情况下，在线式UPS的额定功率越大，故障率越低。在各类故障中，控制电路问题引发的故障占10%左右；晶体管损坏、静电开关失效及充电回路等引发的故障占30%左右；而由电池引发的故障占60%左右。因此，正确使用和维护好电池是降低UPS电源故障的关键，下列哪项的关于UPS的维护管理说法不正确的是（）。

A、定期检查UPS电源免维护电池的端电压和内阻。对于12V单元电池，如果各单元电池间的端电压差超过0.4V以上或其内阻超过8OmΩ时，应对各单元电池进行均衡充电来“复活”电池。

B、定期对电池进行充放电，防止电池因长期没有放电过程而失去活性报废。

C、UPS工作环境应符合要求，温度、湿度适宜，安装规范，放置平稳，接地电阻符合要求，UPS接地电阻小于4Ω计算机直流接地小于1Ω。

D、UPS工作环境应符合要求，温度、湿度适宜，安装规范，放置平稳，接地电阻符合要求，UPS接地电阻小于1Ω计算机直流接地小于4Ω。
查看答案