问题
选择题
已知a,b是正数,且满足2<a+2b<4.那么a2+b2的取值范围是( )
|
答案
以a为横坐标、b为纵坐标,在aob坐标系中作出不等式2<a+2b<4表示的平面区
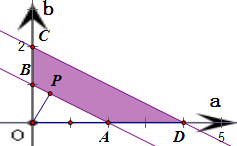
域,
得到如图的四边形ABCD内部,(不包括边界)
其中A(2,0),B(0,1),C(0,2),D(4,0)
设P(a,b)为区域内一个动点,
则|OP|=
表示点P到原点O的距离a2+b2
∴z=a2+b2=|OP|2,
可得当P与D重合时,P到原点距离最远,
∴z=a2+b2<(
)2=1642+02
可得当P点在直线BA上,且满足OP⊥AB时,
P到原点距离最近,等于
=1×2 12+22 2 5 5
∴z=a2+b2>(
)2=2 5 5 4 5
综上所述,可得a2+b2的取值范围是(
,16)4 5
故选:B
