问题
选择题
某家具厂制造甲、乙两种型号的桌子,每张桌子需木工和漆工两道工序完成.已知木工做一张甲、乙型桌子分别需要1小时和2小时,漆工油漆一张甲、乙型桌子分别需要3小时和1小时,又木工、漆工每天工作分别不得超过8小时和9小时,而家具厂制造一张甲、乙型桌子分别获利润20元和30元.试问家具厂可获得的最大利润是( )元.
A.130
B.110
C.150
D.120
答案
设每天生产甲型桌子x张,乙型桌子y张,利润总额为z元.
则 x+2y≤8 3x+y≤9 x≥0 y≥0
目标函数为:z=20x+30y
作出可行域:
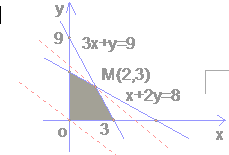
把直线l:2x+3y=0向右上方平移至l'的位置时,直线经过可行域上的点M,且与原点距离最大,此时z=20x+30y取最大值,
解方程
得M的坐标为(2,3).x+2y=8 3x+y=9
此时:z=20×2+30×3=130.
故选:A.

