某垄断厂商的产品在两个分割的市场出售，产品的成本函数和两个市场的需求函数分别为：TC=Q2+10Q，Q1=32-0.4P1，Q2=18-0.1P2。
(1)假设两个市场能实行差别价格，求解利润最大时两个市场的售价、销售量和利润。
(2)假如两个市场只能索取相同的价格，求解利润最大时的售价、销售量和利润。
参考答案：(1)在两个市场上实行差别价格的厂商实现利润最大化的原则是MR1=MR2=MR=MC。
已知Q1=32-0.4P1，即P1=80-2.5Q1，TR1=P1·Q1=80Q1-
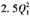，则MR1=80-5Q1。
同理，Q2=18-0.1P2，即P2=180-10Q2，TR2=P2·Q2=180Q2-
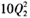，则MR2=180-20Q2。
还知成本函数TC=Q2+10Q，则MC=20+10。
根据MR1=MC，得到80-5Q1=2Q+10，则Q1=14-0.4Q。
同理，根据MR2=MC，得到180-20Q2=2Q+20，则Q2=8.5-0.1Q。
由于Q=Q1+Q2，得到Q=15。
把Q=15代入Q1=14-0.4Q中，得到Q1=8，Q2=Q-Q1=7；
把Q1=8代入P1=80-2.5Q1中，得到P1=60；
把Q2=7代入P2=180-10Q2中，得到P2=110。
利润π=TR1+TR2-TC=P1·Q1+P2·Q2-Q2-10Q=875。
(2)若两个市场价格相等，即P=P1=P2。
已知Q1=32-0.4P1，Q2=18-0.1P2，
所以Q=50-0.5P，即P=100-2Q，则TR=100Q-2Q2，MR=100-4Q。
又从TC=Q2+10q，得MC=2Q+10。
利润最大化的条件是MR=MC，
即100-4Q=2Q+10，从而得到Q=15。
把Q=15代入P=100-2Q中，得到P=70。
利润π=TR-TC=PQ-(Q2-10)=675。