问题
解答题
某工厂生产甲、乙两种产品,这两种产品每千克的产值分别为600元和400元,已知每生产1千克甲产品需要A种原料4千克,B种原料2千克;每生产1千克乙产品需要A种原料2千克,B种原料3千克.但该厂现有A种原料100千克,B种原料120千克.问如何安排生产可以取得最大产值,并求出最大产值.
答案
解析:设生产甲、乙两种产品分别为x千克,y千克,其利产值为z元,
根据题意,可得约束条件为
…(3分)4x+2y≤100 2x+3y≤120 x≥0,y≥0
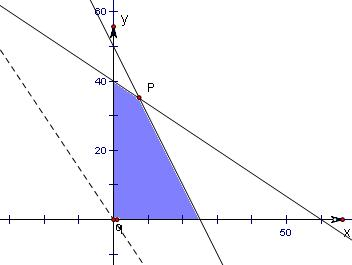
作出可行域如图:….(5分)
目标函数z=600x+400y,
作直线l0:3x+2y=0,再作一组平行于l0的直线l:3x+2y=z,当直线l经过P点时z=600x+400y取得最大值,….(9分)
由
,解得交点P( 7.5,35)….(12分)4x+2y=100 2x+3y=120
所以有z最大=600×7.5+400×35=18500(元)…(13分)
所以生产甲产品7.5千克,乙产品35千克时,总产值最大,为18500元.…(14分)
