问题
填空题
已知函数f(x)=|x2-2|,若f(a)≥f(b),且0≤a≤b,则满足条件的点(a,b)所围成区域的面积为______.
答案
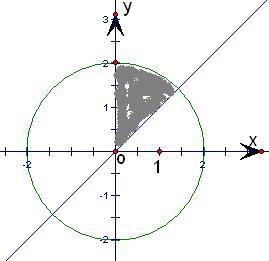
∵由f(x)=|x2-2|,结合f(a)≥f(b)得出(a2-2)2-(b2-2)2≥0,分解为(a2+b2-4)(a-b)(a+b)≥0,
可得约束条件:a 2+b 2≤4 0≤a≤b
其对应的可行域为扇形,如下图示:
其大小为八分之一个圆.
故所求面积为:S=
•4•π=1 8 π 2
故答案为:
.π 2
