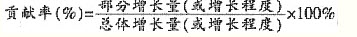已知函数f(x)=x3-3ax(a∈R)
(1)当a=1时,求f(x)的极小值;
(2)若直线x+y+m=0对任意的m∈R都不是曲线y=f(x)的切线,求a的取值范围;
(3)设g(x)=|f(x)|,x∈[-1,1],求g(x)的最大值F(a)的解析式.
(1)∵当a=1时,f′(x)=3x2-3,令f′(x)=0,得x=-1或x=1,当f′(x)<0,即x∈(-1,1)时,f(x)为减函数;当f′(x)>0,即x∈(-∞,-1],或x∈[1,+∞)时,f(x)为增函数.∴f(x)在(-1,1)上单调递减,在(-∞,-1],[1,+∞)上单调递增∴f(x)的极小值是f(1)=-2
(2)∵f′(x)=3x2-3a≥-3a,∴要使直线x+y+m=0对任意的m∈R都不是曲线y=f(x)的切线,当且仅当-1<-3a时成立,∴a<
(3)因g(x)=|f(x)|=|x3-3ax|在[-1,1]上是偶函数,故只要求在[0,1]上的最大值
①当a≤0时,f′(x)≥0,f(x)在[0,1]上单调递增且f(0)=0,∴g(x)=f(x),F(a)=f(1)=1-3a.
②当a>0时,f′(x)=3x2-3a=3(x+)(x-),
(ⅰ)当≥1,即a≥1时,g(x)=|f(x)|=-f(x),-f(x)在[0,1]上单调递增,此时F(a)=-f(1)=3a-1
(ⅱ)当0<<1,即0<a<1时,当f′(x)>0,即x>或x<-时,f(x)单调递增;当f′(x)<0,即-<x<时,f(x)单调递减.所以f(x)在[0,]上单调递减,在[,1]单调递增.
1°当f(1)=1-3a≤0,即≤a<1时,g(x)=|f(x)|=-f(x),-f(x)在[0,]上单调递增,在[,1]上单调递减,F(a)=-f()=2a;
2°当f(1)=1-3a>0,即0<a<
(ⅰ)当-f()≤f(1)=1-3a,即0<a≤时,F(a)=f(1)=1-3a
(ⅱ)当-f()>f(1)=1-3a,即<a<时,F(a)=-f()=2a
综上所述F(x)= | | 1-3a,(a≤) | | 2a,(<a<1) | | 3a-1,(a≥1) |
| |