问题
填空题
在边长为2的正方形ABCD的内部任取一点M,则满足∠AMB>135°的概率为______.
答案
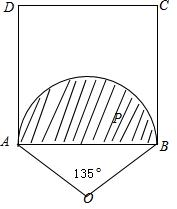
以AB为底边,向正方形外作顶角为135°的等腰三角形,
以等腰三角形的顶点O为圆心,OA为半径作圆,
根据圆周角相关定理,弧AB所对的圆周角为135°.
即当M取圆O与ABCD的公共部分(弓形),∠AMB必大于135°
其中AB=2,OA=
=2 sin 135° 2
,4 2+ 2
O到AB的距离为 2tan
=245° 2
-2,2
故所求的概率为:
S弓形 S正方形
=S扇形-S △AOB S 正方形
=
π×(3 8
)2-4 2+ 2
×2×(21 2
-2)2 2×2
=
,3π(
-1)-22
+22 4
故答案为:3π(
-1)-22
+22 4
