问题
解答题
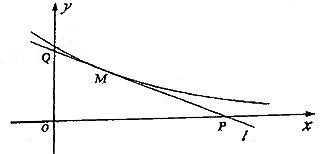
设曲线y=e-x(x≥0)在点M(t,c-1c)处的切线l与x轴y轴所围成的三角表面积为S(t).
(Ⅰ)求切线l的方程;
(Ⅱ)求S(t)的最大值.
答案
(Ⅰ)因为f'(x)=(e-x)'=-e-x,
所以切线l的斜率为-e-1,
故切线l的方程为y-e-t=-e-t(x-t).
即e-tx+y-e-1(t+1)=0
(Ⅱ)令y=0得x=t+1,
又令x=0得y=e-t(t+1)
所以S(t)=
(t+1)•e-1(t+1)1 2
=
(t+1)2e-11 2
从而S′(t)=
e-1(1-t)(1+t).1 2
∵当t∈(0,1)时,S'(t)>0,
当t∈(1,+∞)时,S'(t)<0,
所以S(t)的最大值为S(1)=
.2 e
