问题
填空题
设O为坐标原点，A（1，2），若点B（x，y）满足
|
答案
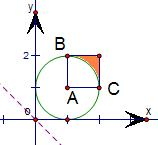
先画出点B（x，y）满足
的平面区域如图，x2+y2-2x-2y+1≥0 1≤x≤2 1≤y≤2.
又因为
•OA
=x+2y．OB
所以当在点C（2，1）处时，x+2y最小．
即满足要求的点是（2，1）．
故答案为：（2，1）．
搜题请搜索小程序“爱下问搜题”
设O为坐标原点，A（1，2），若点B（x，y）满足
|
先画出点B（x，y）满足
的平面区域如图，x2+y2-2x-2y+1≥0 1≤x≤2 1≤y≤2.
又因为
•OA
=x+2y．OB
所以当在点C（2，1）处时，x+2y最小．
即满足要求的点是（2，1）．
故答案为：（2，1）．
