问题
问答题
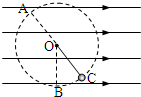
如图所示,在水平向右的匀强电场中,有一个带电小球,用长为0.2m的绝缘细线悬挂在O点,当小球静止在C点时,细线与竖直方向夹角为60°.若小球恰能在竖直平面内做完整的圆周运动,g=10m/s2,求:
(1)小球运动过程中的最小速度;
(2)小球运动到O点正下方B点时的速度.
答案
(1)小球在C点受重力、电场力和拉力处于平衡,知电场力和重力的合力与拉力等值反向,知A点为圆周运动的等效最高点.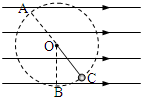
根据牛顿第二定律得:
=mmg cos60° v12 r
解得最小速度为:v1=
=gr cos60°
m/s=2m/s.10×0.2 1 2
(2)对小球从A点到B点运用动能定理得:qErsin60°+mgr(1+cos60°)=
mv22-1 2
mv121 2
因为tan60°=
,则qE=qE mg
mg3
代入解得:v2=4m/s.
答:(1)小球运动过程中的最小速度2m/s
(2)小球运动到O点正下方B点时的速度4m/s
