问题
填空题
如果直线y=kx+1与圆x2+y2+kx+my-4=0相交于M、N两点,且点M、N关于直线x+y=0对称,动点P(a,b)在不等式组
(1)不等式组所确定的平面区域的面积为1; (2)使得目标函数z=b-a取得最大值的最优解有且仅有一个; (3)目标函数ω=
(4)目标函数p=a2+b2-2b+1的最小值是
上述说法中正确的是______(写出所有正确选项) |
答案
∵M、N两点,关于直线x+y=0对称,
∴k=1,又圆心(-
,-k 2
)在直线x+y=0上m 2
∴-
-k 2
=0m 2
∴m=-1
∴原不等式组变为
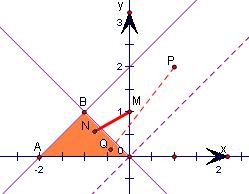
作出不等式组表示的平面区域,x-y+2≥0 x+y≤0 y≥0
(1)△AOB为不等式所表示的平面区域,
联立
解得B(-1,1),A(-2,0),y=-x y=x+2
所以S△AOB=
×|-2|×|-1|=1.1 2
故(1)正确;
(2)作出目标函数z=b-a平行的直线,将其平移
当直线z=b-a过直线x-y+2=0上的任一点时,z最大,
故(2)错;
(3)如图
又因为ω=
表示点P(a,b)与点(1,2)连线的斜率.b-2 a-1
故当过点B(-1,1)时,ω=
取最小值-b-2 a-1
.1 2
当过O(0,0)时,ω=
取最大值2.b-2 a-1
故答案为:[-
,2].故(3)错;1 2
(4)p=a2+b2-2b+1=a2+(b-1)2-表示区域内的点N到点M(0,1)的距离的平方,
由图得:只有当过M作直线x+y=0的垂线时,M(0,1)到平面区域内任一点的距离才最小.
而M与直线x+y=0的距离为:d=
=|0+1| 12+12
.1 2
∴|d|2=
.即目标函数p=a2+b2-2b+1的最小值是1 2
.1 2
故(4)正确.
故答案为:(1),(4).
