问题
计算题
如图甲所示,固定在竖直平面内的光滑轨道由倾斜部分AB和CD以及圆弧部分BC组成,轨道AB和CD分别与圆弧部分BC相切于B、C两点,圆弧BC所对应的圆心角为74°,整个轨道关于复运动,已知滑块对轨道的压力大小F随时间t的变化规律如图乙所示。(g取10m/s2)试求:
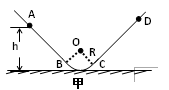
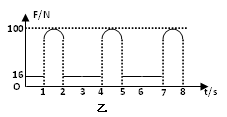
小题1:压力大小F随时间t变化的周期与小滑块做往复运动的周期之比
小题2:滑块的质量
小题3:倾斜轨道AB部分的长度L
小题4:圆弧轨道的半径R
答案
小题1: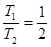
小题2:m=2kg
小题3:L=at2/2="3m "
小题4:R=1m
①(4分)由图乙可知,压力大小F随时间t变化的周期T1="3s " (2分)
滑块从A点出发至回到A点所需的时间T2=6s,即为滑块运动的周期
二者之比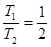 (2分)
(2分)
②(4分)由图乙可知,滑块在斜面上运动时对轨道的压力F1=16N,
受力分析可知F1=mgcosθ (2分)
其中,θ=74°/2=37°。可得,滑块的质量m="2kg " (2分)
③(4分)滑块在倾斜轨道上做匀加速直线运动,加速度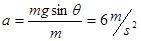 (2分)
(2分)
由图乙可知,滑块滑行的时间t1=1s,故AB的长L=at2/2="3m " (2分)
④(6分)设滑块经过最低点时的速度为v,由机械能守恒可得:
mgh=mv2/2 (2分)
而h=Lsinθ+R(1-cosθ) (1分)
由图乙可知,滑块对轨道的压力F2=100N
滑块在最低点处由牛顿第二定律可得: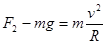 (2分)
(2分)
联立解得:R="1m " (1分)
