问题
计算题
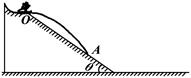
如下图所示，高台滑雪运动员经过一段滑行后从斜坡上的O点水平飞出，斜坡与水平面的夹角θ=37°，运动员连同滑雪板的总质量为m=50kg，他落到斜坡上的A点后不再弹起，立即顺势沿斜坡下滑。A点与O点的距离为S1=12m，A点与斜面底端的距离为S2=5.6m，滑雪板与斜坡和水平面上的动摩擦因数均为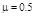
，运动员滑到斜面底端时仅速度方向变为水平，大小不变。忽略空气阻力，重力加速度g=10m/s2。（sin37°=0.6；cos37°=0.8），求：
小题1:运动员从O点运动到斜面底端需要多长时间？
小题2:运动员在水平面上能滑行多远？
答案
小题1:1.6s；
小题2:20.7m
（1）设运动员在空中飞行时间为t1，运动员在竖直方向做自由落体运动，得
S1sin37°=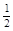
gt12（1分）解得：
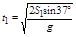="1.2s" （1分）
故到A点时竖直方向的速度为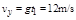
（1分）
设运动员离开O点的速度为vx，运动员在水平方向做匀速直线运动，即S1cos37°=vxt1 （1分）
解得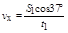
="8.0m/s" （1分）
故运动员落到A点后沿斜面下滑的初速度为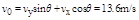
（1分）
沿斜面下滑时有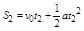
（1分）
根据牛顿第二定律有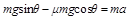
（1分）
解得t2="0.4s" （1分）
故运动员从O点到斜面底端需要的时间为t=t1+t2=1.6s（1分）
（2）运动员到达斜面底端的速度为v=v0+at2（1分）
运动员到达水平面后做减速运动，加速度大小为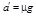
（1分）
故运动的距离为S＇=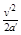
（1分）
联立解得S＇="20.7m" （1分）