问题
选择题
f（x）＝x3+ax2+bx+a2在x＝1有极值10，那么a+b的值为 （ ）
A．－7
B．0
C．－7或0
D．不确定
答案
Ａ
∵f′（x）＝3x2+2ax+b，由已知得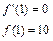
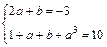
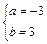
或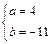
，
当a＝－3，b＝3时，f ′（x）＝
3（x－1）2≥0，此时x＝1不是极值点．
当a＝4，b＝－11时，易验证x＝1是f（x）的极小值点，故选A．
搜题请搜索小程序“爱下问搜题”
f（x）＝x3+ax2+bx+a2在x＝1有极值10，那么a+b的值为 （ ）
A．－7
B．0
C．－7或0
D．不确定
Ａ
∵f′（x）＝3x2+2ax+b，由已知得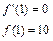
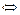
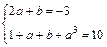
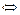
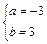
或，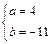
当a＝－3，b＝3时，f ′（x）＝3（x－1）2≥0，此时x＝1不是极值点．
当a＝4，b＝－11时，易验证x＝1是f（x）的极小值点，故选A．