如图1所示，真空中存在电场强度E=1.5×103V/m、方向竖直向上的匀强电场．在电场中固定有竖直面内的光滑绝缘轨道ABC，其中AB段水平，BC段是半径R=0.5m的半圆，直径BC竖直．有两个大小相同的金属小球1和2（均可视为质点），小球2的质量m2=3×10-2kg、电量q=+2×10-4C，静止于B点；小球1的质量m1=2×10-2kg、不带电，在轨道上以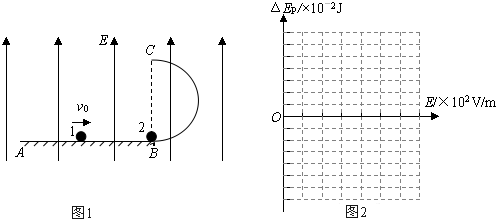
初速度v0=m/s向右运动，与小球2发生弹性正碰，碰撞时间极短，取g=10m/s2，求：
（1）碰撞后瞬间小球2的速度v2的大小
（2）小球2经过C点时，轨道对它的压力FN的大小以及它第一次落到轨道AB上的位置距B点的距离x
（3）若只改变场强E的大小，为了保证小球2能沿轨道运动并通过C点，试确定场强E的取值范围；并在图2的坐标系中，画出小球2由B点沿轨道运动至C点的过程中，其电势能变化量△EP与场强E的关系图象（画图时不必说明理由）
（1）设两小球碰撞后的速度速度分别为v1、v2，则
m1v0=m1v1+m2v2
弹性碰撞，无机械能损失，故：
m1=m1+m2
解得：
v2===2m/s
（2）设小球2经过C点时速度为v2′，由动能定理，有：
（E-m2g)•2R=m2-m2•2R=m2-m2
解得：
v2′=m/s
又FN+m2g-E=m2
得：
FN=m2-m2g+E=m2-5m2g+qE
代入数据得：
FN=0.45N
小球2离开C点后做类平抛运动，加速度：
a==g=5m/s2
2R=at2
解得：
t=
所以x=v′2t=×=2m
（3）在上述（2）中，令FN≥0，即有
m2-5m2g+qE≥0
E≥==600V/m
又由题设有：qE≤m2g
E≤==1.5×103V/m
故满足题目要求的场强E大小的取值范围是：
0.6×103≤E≤1.5×103V/m
电势能变化量△E与场强E的关系图象如图：
答：（1）碰撞后瞬间小球2的速度v2的大小为2m/s；
（2）小球2经过C点时，轨道对它的压力FN的大小为0.45N，它第一次落到轨道AB上的位置距B点的距离x为2m；
（3）场强E的取值范围为：0.6×103≤E≤1.5×103V/m；
小球2由B点沿轨道运动至C点的过程中，其电势能变化量△EP与场强E的关系图象如图所示．
