问题
解答题
甲、乙两船驶向一个不能同时停泊两艘船的码头,它们在一天二十四小时内到达该码头的时刻是等可能的.如果甲船停泊时间为1小时,乙船停泊时间为2小时,求它们中的任意一艘都不需要等待码头空出的概率.
答案
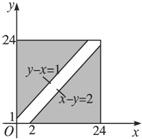
这是一个几何概型问题.
设甲、乙两艘船到达码头的时刻分别为x与y,A为“甲、乙两船都不需要等待码头空出”,
则0≤x≤24,0≤y≤24,
且基本事件所构成的区域为Ω={(x,y)|0≤x≤24,0≤y≤24}.
要使两船都不需要等待码头空出,
当且仅当甲比乙早到达1小时以上或乙比甲早到达2小时以上,
即y-x≥1或x-y≥2,故A={(x,y)|y-x≥1或x-y≥2},x∈[0,24],y∈[0,24].
A为图中阴影部分,Ω为边长是24的正方形,
∴所求概率P(A)=A的面积 Ω的面积
=(24-1)2×
+(24-2)2×1 2 1 2 242
=
=506.5 576
.1013 1152
