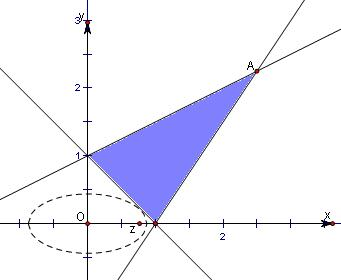
根据约束条件画出可行域
z=x²+4y²表示中心在坐标原点，焦点在x轴上的椭圆，如图．

当此椭圆与直线x+y=1相切时，z=x²+4y²最小，

由

z=x2+4y2 x+y=1

消去x得：5y²-2y+1-z=0，

△=0得z=

4

5

，即最小距离为

4

5

，
当此椭圆过点A（

5

2

，

9

4

）时，z=x²+4y²最大，最大为z=（

5

2

）²+4（

9

4

）²=

53

2

．
故答案为：[

4

5

，

53

2

]．