问题
填空题
已知f（x）=x2-2x，则满足条件
|
答案
∵f（x）=x2-2x
∴约束条件f(x)+f(y)≤0 f(x)-f(y)≥0
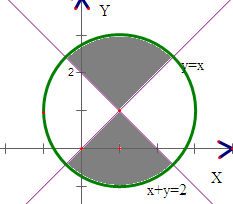
可以转化为(x-1)2+(y-1)2≤2 (x-1)2-(y-1)2≥0
其对应的可行域如下图示：
其面积为：
•π•1 2
2=π2
故答案为：π
搜题请搜索小程序“爱下问搜题”
已知f（x）=x2-2x，则满足条件
|
∵f（x）=x2-2x
∴约束条件f(x)+f(y)≤0 f(x)-f(y)≥0
可以转化为(x-1)2+(y-1)2≤2 (x-1)2-(y-1)2≥0
其对应的可行域如下图示：
其面积为：
•π•1 2
2=π2
故答案为：π