问题
问答题
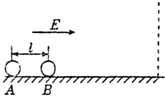
如图所示,在一光滑绝缘水平面上,静放着两个可视为质点的小球,两小球质量均为m,相距l,其中A带正电,所带电荷量为q,小球B不带电.若加一水平向右的匀强电场,场强为E,A球受到电场力的作用向右运动与B球碰撞.设每次碰撞前后两球交换速度,且碰撞过程无电荷转移.若两小球恰在第三次碰撞时离开电场,求:
(1)小球A在电场中的加速度大小;
(2)小球A在电场中运动的距离.
答案
(1)由牛顿第二定律得:加速度a=
=F m
,qE m
(2)以A为研究对象,由动能定理得:qEL=
m1 2
,v 21
解得:两球第一次碰撞前瞬间,A球速度:v1=
=2qEL m
;2aL
两球第一次碰撞后瞬间,A球速度0,B球速度v1.
碰后A做匀加速直线运动,B做匀速直线运动,当它们位移相等时再次发生碰撞,
两球第二次碰撞前瞬间,有v1t1=
a1 2 t 21
解得:t1=
,2v1 a
此时A球速度:v2=at1=2v1,
两球第二次碰撞后瞬间,A球速度v1,B球速度v2=2v1,
两次碰撞之间A的位移S2:2as2=
-0=4v 22 v 21
所以:s2=4L
位移相等,得:v2t2=v1t2+
a1 2
,t 22
得:t2=2v1 a
两次碰撞之间A的位移S3
s3=v1t2+
a1 2 t 22
代入数据得:s3=8L
小球A在电场中运动的距离:x=L+s2+s3=13L
答:(1)小球A在电场中的加速度大小a=
;qE m
(2)小球A在电场中运动的距离为13L.
