问题
问答题
如图所示,等量异种点电荷相距为2L,固定在水平线上的M、N两点,电荷量均为Q.有一带正电的小球质量为m,电荷量q(可视为点电荷),固定在长为L的绝缘轻质细杆的一端,杆的另一端可绕光滑轴0转动,0在MN的垂直平分线上方距MN为L处.现在把杆拉至水平(与MN平行)并由静止释放,运动中经过最低点B时,小球的速度为v.已知静电力常量为k,取O处电势为零,忽略q对+Q、-Q形成电场的影响,求:
(1)在+Q、-Q形成的电场中,A点的电势φA
(2)小球经过B点时对细杆的拉力大小
(3)小球继续向左摆动,能否经过与A等高度的C点(OC=L)?若能,求出此时的速度;若不能,请说明理由.
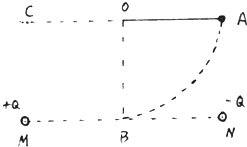
答案
(1)由于取O点电势为零,而O在MN的垂直平分线上,所以φB=0
电荷从A到B过程中,由动能定理得:mgL+(φA-φB)=
mv21 2
得:φA=mv2-2mgL 2q
(2)小球经B点时,在竖直方向有
T-mg=mv2 L
T=mg+mv2 L
由牛顿第三定律知,小球对细杆的拉力大小也为mg+mv2 L
(3)小球不能经过C处
因为在+Q,-Q形成的电场中,φC>φA,假设小球能经过C处,则q(φA-φC)=
mv2,有1 2
<0所以不可能.v 2C
答:(1)A点的电势φA=
;mv2-2mgL 2q
(2)小球经过B点时对细杆的拉力大小mg+
;mv2 L
(3)小球继续向左摆动,不能否经过与A等高度的C点(OC=L).
