问题
解答题
(本小题满分12分)
有一块边长为6m的正方形钢板,将其四个角各截去一个边长为x的小正方形,然后焊接成一个无盖的蓄水池。
(Ⅰ)写出以x为自变量的容积V的函数解析式V(x),并求函数V(x)的定义域;
(Ⅱ)指出函数V(x)的单调区间;
(Ⅲ)蓄水池的底边为多少时,蓄水池的容积最大?最大容积是多少?
答案
(Ⅰ)x∈(0,3) (Ⅱ)(0,1),(1,3) (Ⅲ)4m时,其最大容积是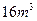
(Ⅰ)设蓄水池的底面边长为a,则a="6-2x,"
则蓄水池的容积为: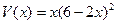 .
.
由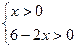 得函数V(x)的定义域为x∈(0,3). ………4分
得函数V(x)的定义域为x∈(0,3). ………4分
(Ⅱ)由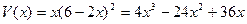 得
得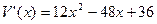 .
.
令 ,解得x<1或x>3;
,解得x<1或x>3;
令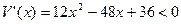 ,解得1<x<3.
,解得1<x<3.
故函数V(x)的单调增区间是(0,1),单调减区间为(1,3). ………8分
(Ⅲ)令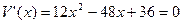 ,得x=1或x=3(舍).
,得x=1或x=3(舍).
并求得V(1)="16. " 由V(x)的单调性知,16为V(x)的最大值.
故蓄水池的底边为4m时,蓄水池的容积最大,其最大容积是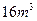 . ………12分
. ………12分
