问题
填空题
若曲线y=x3-2x+a与直线y=4x+1相切,则常数a的值为___________.
答案
1+4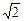 或1-4
或1-4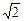
本题考查导数的几何意义.先求导数,令导数等于切线的斜率,从而求出切点坐标,代入原方程,从而求得常数a.
y′=3x2-2.
令3x2-2=4,解得x1=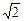 或x2=-
或x2=-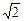 .
.
所以切点坐标分别为(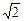 ,4
,4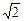 +1),(-
+1),(-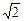 ,-4
,-4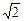 +1).
+1).
把x1=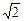 ,y1=4
,y1=4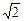 +1代入y=x3-2x+a中,得a1=4
+1代入y=x3-2x+a中,得a1=4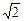 +1;
+1;
把x2=-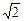 ,y2=-4
,y2=-4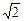 +1代入y=x3-2x+a中,得a2=-4
+1代入y=x3-2x+a中,得a2=-4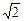 +1.
+1.
